 MÉTODOS PARA LA DETERMINACIÓN DE
FRECUENCIAS
 Introducción
Bases matemáticas
Fiabilidad: conceptos básicos
Determinación de la tasa de fallo de un
suceso básico
 Consideraciones generales
 Banco de datos de fiabilidad de
componentes
Determinación del fallo humano
Determinación de frecuencias de
sucesos complejos
|
2.4.2 Banco
de datos de fiabilidad de componentes
En
la tabla 2.5 se describen algunos de los bancos de datos de fiabilidad más
destacados.
|
TABLA
2.5 BANCOS DE DATOS DE FIABILIDAD DE COMPONENTES |
* United
Kinqdom Atomic Energy Agency.
** Ente Nazionale
d'Idrocarburi.
*** Offshore
REliability DAta.
De
esta tabla se desprenden los siguientes comentarios:
-
Existen pocos bancos de datos de procedencia exclusivamente química.
-
os datos de procedencia «nuclear» deben ser utilizados con el
debido cuidado ya que por sus características son relativamente distintas.
-
Los bancos de datos dan en general una medida de la incertidumbre que
pesa sobre el dato acotándolo en un intervalo de variación. En general, el
modelo utilizado para describir la incertidumbre asociada a la tasa de fallo
λ
consiste en considerarla como una variable aleatoria que sigue una
ley de densidad de tipo lognormal caracterizada por su media λm
(igual a la mediana) y un factor de error f. La tasa de fallos se concentra
con un 90% de probabilidad entre un valor máximo (λm x f) y
mínimo (λm/f). En el esquema que sigue se representa la ley
de distribución de la variable aleatoria «tasa de fallos» señalándose
en abcisas los valores de la tasa y en ordenadas las probabilidades de
obtener estos valores.
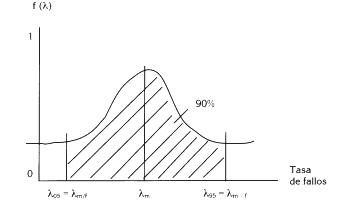
donde:
 |
λm:
mediana de la distribución lognormal (su probabilidad acumulada es
del 50%). |
|
λ05:
valor de la tasa de fallos para el cual la probabilidad acumulada de
obtener un valor más pequeño es del 5%. |
|
λ95:
valor de la tasa de fallos para el cual la probabilidad de obtener un
valor inferior o igual es del 95%. |
|
¦(λ ): función de densidad de la ley de distribución de la
variable
aleatoria tasa de fallos. |
|
///: área con una probabilidad acumulada del 90% de
que la tasa de
fallos, se halla dentro del rango [l05;
l95]
(abcisas de
las rectas verticales que delimitan el área). |
Los
cálculos de frecuencia deben de tomar en consideración estos intervalos de
variación de la tasa de fallos.
Ver
apartado «Análisis de incertidumbre» en 2.5. 1.1 C). |
